Layered Nonlinear Model Predictive Control for Robust Stabilization of Hybrid Systems
Abstract
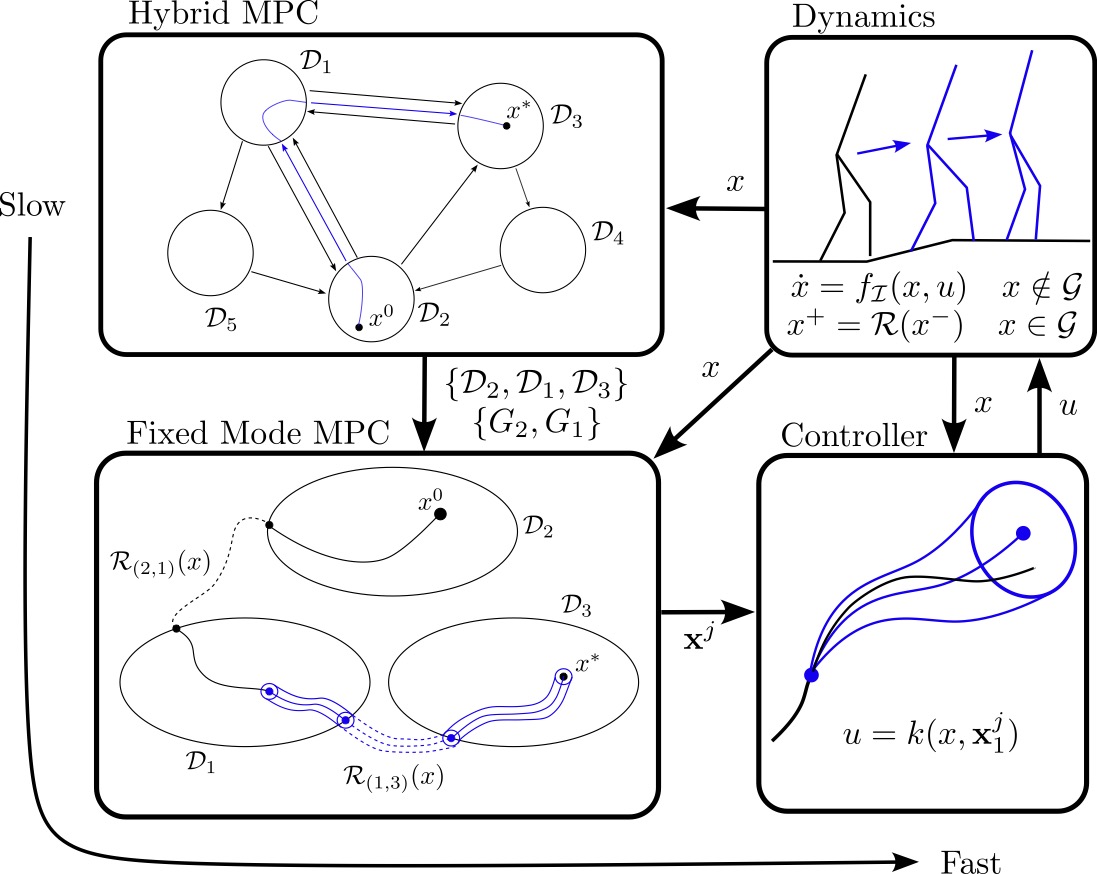
Computing the receding horizon optimal control of nonlinear hybrid systems is typically prohibitively slow, limiting real-time implementation. To address this challenge, we propose a layered Model Predictive Control (MPC) architecture for robust stabilization of hybrid systems. A high level “hybrid” MPC is solved at a slow rate to produce a stabilizing hybrid trajectory, potentially sub-optimally, including a domain and guard sequence. This domain and guard sequence is passed to a low level “fixed mode” MPC which is a traditional, time-varying, state-constrained MPC that can be solved rapidly, e.g., using nonlinear programming (NLP) tools. A robust version of the fixed mode MPC is constructed by using tracking error tubes that are not guaranteed to have finite size for all time. Using these tubes, we demonstrate that the speed at which the fixed mode MPC is re-calculated is directly tied to the robustness of the system, thereby justifying the layered approach. Finally, simulation examples of a five link bipedal robot and a controlled nonlinear bouncing ball are used to illustrate the formal results.
Additional Info
Authors: Zachary Olkin, Aaron Ames
Conference: ACC 2025 (American Control Conference)
Location of work: Amber Lab, Caltech
Dates of work: May 2024 - September 2024
Paper: arxiv
Github. Note that the code was not designed as a library. This is just the code to re-create the examples.